CF1324F Maximum White Subtree 题解

传送门: F. Maximum White Subtree

给予你一颗无根树，树上的节点被染成黑色或者白色，求对于某一个节点，在任意包含这个节点的子树中，问白色的节点数量最多能比黑色节点多多少个？

例：

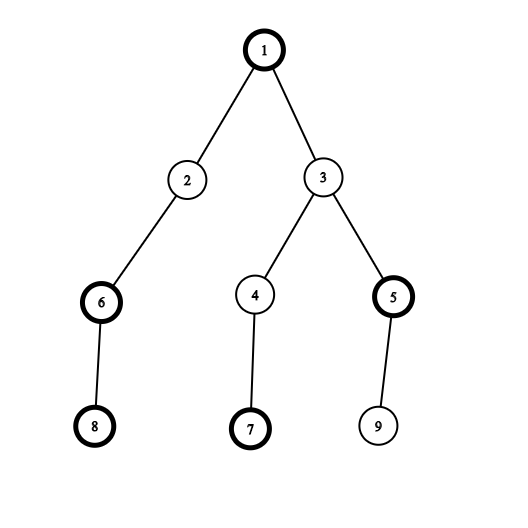
黑色节点为加粗边框的节点

对于节点4，答案为2，选的子树为$(3,4)$

对于无根树，应该先想的转换成有根树，不妨设根节点为1

对于根节点，其答案只与他的子节点有关，我们定义$f_u$：在以节点1为根节点的条件下，在以节点$u$为根的子树中，选择一个包含节点$u$的树，白色节点能比黑色节点多的最大数量。用样例中的节点3举例，这里的子树为$(3,4,7,5,9)$，所以$f_3$为2，选的树为$(3,4)$

至此，基本的DP思路就出来了，对于一个节点$u$，便利一下$u$的子节点$v$，若是在以$v$为根的子树中，通过选择白色节点能比黑色节点多，即$f_v$非负，那我们就可以（应该）选择加上$v$这个节点以及$v$选中的子节点以及$v$选中的子节点选中的子节点……（禁止套娃），但是我们只关心数量，不关心选中了哪些节点。综上就有了下面这个DP方程：

对于某个节点$u$

$$f_u=colour_u+\sum_{\text v \in \text{Subtree}(u)}max(f_v, 0)$$

其中$colour_u$代表节点$u$对于答案的贡献值，若$u$为白色节点，则$colour_u$为1，否则为-1

至此我们就得到了一个朴素的解法：让每个点都做一次根节点，跑一次上述所说的DP，复杂度为$O(n^2)$，可惜是过不了的，我们还得找新的解法

通过观察我们可以发现，对于非根节点，整棵树除去以这个节点为根的子树的余下部分可能对答案也有影响，例如样例中的节点9。我们定义$g_u$：在以节点1为根节点的条件下，在整棵树除去以节点$u$为根的子树中（但是保留节点$u$），选择一个包含节点$u$​的树，白色节点能比黑色节点多的最大数量。用样例中的节点3举例，这里的树为$(3,1, 2, 6, 8)$，所以$g_3$为1，选的树为$(3)$或者$(3, 1, 2)$

然后就是思考如何能够推出$gu$，通过观察我们可以发现，$g{fa(u)}$和$g_u$其实有公共部分，如下图：

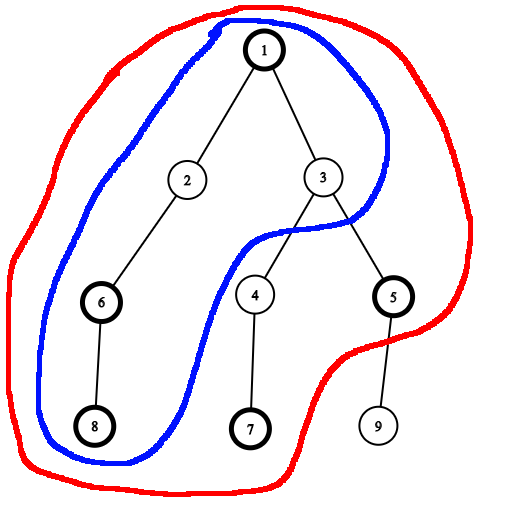
当$u=5$时，红色区域表示$gu$，蓝色区域表示$g{fa(u)}$，两者差了一个$colour_u$和$fa(u)$的若干个子节点对于答案的影响，所以我们可以推出关于$g$的DP方程：

对于某个节点$u$

$$g_u=colour_u+max(g_{fa(u)}+\sum_{\text v \in \text{Subtree(fa(u)) and v} \neq \text{u}} max(f_v, 0), 0)$$

但是要递推这个DP的复杂度为$O(n^2)$，我们必须优化一下。可以注意到，在这个方程中后面的一部分和$f$的DP方程类似，考虑从这块入手：

$$f_{fa(u)}-colour_{fa(u)}=\sum_{\text v \in \text{Subtree(fa(u))}} max(f_v, 0)=\sum_{\text v \in \text{Subtree(fa(u)) and v} \neq \text{u}} max(f_v, 0)+max(f_u, 0)$$

把右边的$max(f_u, 0)$移到左边去：

$$\sum_{\text v \in \text{Subtree(fa(u)) and v} \neq \text{u}} max(f_v, 0)=f_{fa(u)}-colour_{fa(u)}-max(f_u, 0)$$

代回$g$的DP方程：

$$g_u=colour_u+max(g_{fa(u)}+f_{fa(u)}-colour_{fa(u)}-max(f_u, 0), 0)$$

因为$f$在推$g$的时候应该已经计算完成了，所以只需便利一遍图便可推出$g$，复杂度$O(n)$

而计算答案$ans_u$的时候本应该将$f$和$g$相加，但是$colour_u$会被重复计算一次，所以要减掉：

$$ans_u=f_u+max(g_u-colour_u, 0)$$

#include<bits/stdc++.h>
#define pll pair<ll, ll>
using namespace std;
typedef long long ll;

int n;

void dfsf(int u, int fa, vector<vector<int>> &G, vector<int> &f, vector<int> &colour){
    int sum=0;

    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa) continue;

        dfsf(v, u, G, f, colour); //注意这里要在求和之前先把子节点算完

        sum+=max(f[v], 0);
    }

    f[u]=colour[u]+sum;
}

void dfsg(int u, int fa, vector<vector<int>> &G, vector<int> &f, vector<int> &g, vector<int> &colour, vector<int> &ans){
    g[u]=colour[u]+max(0, g[fa]+f[fa]-max(0, f[u])-colour[fa]);
    ans[u]=f[u]+max(0, g[u]-colour[u]);

    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(v==fa) continue;

        dfsg(v, u, G, f, g, colour, ans);
    }
}

void Main(int kase){
    cin>>n;

    vector<int> colour(n+1), f(n+1), g(n+1), ans(n+1);
    vector<vector<int>> G(n+1, vector<int>());

    for(int i=1;i<=n;i++){
        cin>>colour[i];

        if(colour[i]==0) colour[i]=-1;
    }

    int u, v;
    for(int i=1;i<n;i++){
        cin>>u>>v;

        G[u].push_back(v);
        G[v].push_back(u);
    }

    dfsf(1, 0, G, f, colour);
    dfsg(1, 0, G, f, g, colour, ans);

    for(int i=1;i<=n;i++){
        cout<<ans[i]<<" ";
    }
    cout<<endl;
}

int main(){
    #ifdef DEBUG
    freopen("in.txt", "r", stdin);
    #endif
    
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    Main(1);
    
    return 0;
}