CF1734D Slime Escape 题解

传送门：Slime Escape

一条直线上有$n(3 \leq n \leq 200000)$个史莱姆，你能控制第$k(1 \leq k \leq n)$个，第$i$个史莱姆的生命值是$a_i$。

现在你可以控制这个史莱姆向左或者向右“吞噬”别的史莱姆，你每“吞噬”一个史莱姆$i$，你控制的史莱姆的生命值会增加$a_i$，但是有的史莱姆的生命值是负的，一旦你控制的史莱姆的生命值也变成负的话，你就输掉了游戏。

通关的目标是走到最左边或者走到最右边，问你有没有可行的解。

第一眼看到这道题本来以为是道水题（？），不断的吞噬最相邻的两个史莱姆，直到出去，但是 wrong answer test case 2了

1800的题哪有这么水的

正解是以你操纵的那个史莱姆为中心，不断地往外划分区块。一共有两种不同的区块类型：

1. 区块里的数字之和是非负数的区块
2. 除了第一种区块，两边可能会剩下一些和不是非负数但是吞掉这个区块就能通关的

每个区块要记一个最低吞噬的生命值，这也很好理解。对于第一个区块，如果能够吞噬，那肯定选择吞掉，这样可以获得更多的生命值来通关；第二种如果能吞掉就直接通关了。

这是第三个样例的区块划分：

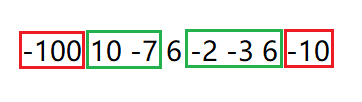
预处理好之后能吞就吞，如果没有能吞的之后还是没有通关，则不可能通关

ll n, k;

void Main(int kase){
	cin>>n>>k;
	vector<ll> A(n+1);
	for(ll i=1;i<=n;i++) cin>>A[i];

	queue<pll> Q1, Q2;
	ll sum=0, mn=LLONG_MAX;
	for(ll i=k-1;i>=1;i--){
		sum+=A[i];
		mn=min(mn, sum);

		if(sum>=0){
			Q1.push(make_pair(sum, -mn));
			sum=0;
			mn=LLONG_MAX;
		}
	}
	Q1.push(make_pair(sum, -mn));
	sum=0;
	mn=LLONG_MAX;
	for(ll i=k+1;i<=n;i++){
		sum+=A[i];
		mn=min(mn, sum);

		if(sum>=0){
			Q2.push(make_pair(sum, -mn));
			sum=0;
			mn=LLONG_MAX;
		}
	}
	Q2.push(make_pair(sum, -mn));
	sum=0;
	mn=LLONG_MAX;

	ll cur=A[k];
	while(!Q1.empty() && !Q2.empty()){
		if(cur<Q1.front().second && cur<Q2.front().second){
			cout<<"NO"<<endl;
			return;
		}

		while(!Q1.empty() && cur>=Q1.front().second) cur+=Q1.front().first, Q1.pop();
		while(!Q2.empty() && cur>=Q2.front().second) cur+=Q2.front().first, Q2.pop();
	}

	cout<<"YES"<<endl;
}