Effiziente Algorithmen und Datenstrukturen II

EA2的笔记

（感谢fy的课后辅导）

Introduction to Linear Programming (LP)

给定$m$个对于$n$个自变量的约束条件, 要求在满足这些约束条件的前提下, 最大化收益.

标准的LP形式:

$$\begin{aligned} & \max \left( \sum_{j=1}^n c_j x_j \right) \\ & \text { s.t. } \sum_{j=1}^n a_{i j} x_j=b_i \quad 1 \leq i \leq m \\ & x_j \geq 0 \quad 1 \leq j \leq n \\ & \end{aligned}$$

以数组的形式:

$$\begin{aligned} \max & \left(c^T x\right) \\ \text { s.t. } & A x=b \\ & x \geq 0 \end{aligned}$$

其中$Ax=b$指出了自变量$x$需要满足的条件, 而$c^Tx$就是收益计算方式, 他给每一个自变量$x_j$一个权值$c_j$.

当然, LP也有除了等号的标准形式:

• 求最小值: $\begin{array}{rr} & \min \left( c^T x \right) \ & \text { s.t. } A x=b \ & x \geq 0\end{array}$
• 最大化约束: $\begin{array}{rr} & \max \left( c^T x \right) \ & \text { s.t. } A x \leq b \ & x \geq 0\end{array}$
• 最小化约束: $\begin{array}{rr} & \max \left( c^T x \right) \ & \text { s.t. } A x \geq b \ & x \geq 0\end{array}$

我们可以很容易地从一个形式转换成另一个形式:

• 小于等于变等于: $a-3 b+5 c \leq 12 \Rightarrow \begin{aligned} a-3 b+5 c+s & =12 \ s & \geq 0\end{aligned}$
• 大于等于变等于: $a-3 b+5 c \geq 12 \Rightarrow \begin{aligned} a-3 b+5 c-s & =12 \ s & \geq 0\end{aligned}$
• 最小值转最大值: $\min \left( a-3 b+5 c \right) \Rightarrow \max \left( -a+3 b-5 c \right)$
• 等于转小于等于: $a-3 b+5 c=12 \Rightarrow \begin{gathered}a-3 b+5 c \leq 12 \ -a+3 b-5 c \leq-12\end{gathered}$
• 等于转大于等于: $a-3 b+5 c=12 \Rightarrow \begin{gathered}a-3 b+5 c \geq 12 \ -a+3 b-5 c \geq-12\end{gathered}$
• 未限制转非负: $x$ unrestricted $\Rightarrow x=x^{+}-x^{-}, x^{+} \geq 0, x^{-} \geq 0$

只要是新加的变量都有非负的限制条件, 这是因为自变量$x_j$必须是非负的

Definition 1 (Linear Programming Problem (LP))

已知 $A \in \mathbb{Q}^{m \times n}, b \in \mathbb{Q}^m, c \in \mathbb{Q}^n, \alpha \in \mathbb{Q}$, 问是否存在 $x \in \mathbb{Q}^n$ s.t. $A x=b, x \geq 0$, 使得 $ c^T x \geq \alpha$ ?

LP $\in$ NP / co-NP / P ?

• LP是NP问题吗？
• LP是co-NP问题吗？
• LP是P问题吗？

输入

$n$是自变量的数量, $m$是约束条件的数量, $L$是编码输入需要的bit.

LP的几何意义

一些额外的定义

对于一个满足条件的自变量的集合 $P={x \mid A x=b, x \geq 0}$:

• $P$ 被称作可行域(feasible region)
• $P$ 中的一个点$x \in P$被称作可行解(feasible point)
• 如果 $P \neq \varnothing$ , 那这个LP就被称作可解的(feasible), 否则就是无解的(infeasible)
• LP是有界的(bounded)如果它是有解的并且
• • 所有可行解 $x \in P$ , $c^T x<\infty$
• • 所有可行解 $x \in P$ , $c^T x>-\infty$

Definition 2

给定向量或者点 $x_1, \ldots, x_k \in \mathbb{R}^n$ , $\sum \lambda_i x_i$:

• 线性组合(linear combination), 如果 $\lambda_i \in \mathbb{R}$
• 仿射组合(affine combination), 如果 $\lambda_i \in \mathbb{R}$ 并且 $\sum_i \lambda_i=1$
• 凸组合(convex combination), 如果 $\lambda_i \in \mathbb{R}$, $\sum_i \lambda_i=1$ 并且 $\lambda_i \geq 0$
• 锥组合(conic combination), 如果 $\lambda_i \in \mathbb{R}$ 并且 $\lambda_i \geq 0$

组合中的向量或者点的个数必须是有限的!!!

Definition 3 & 4

集合$X \subseteq \mathbb{R}^n$是:

• $span(X)$ : 线性子空间(linear subspace), 如果它在线性组合下是个闭集(closed set)
• $aff(X)$ : 仿射子空间(affine subspace), 如果它在仿射组合下是个闭集
• $conv(X)$ : 凸包(convex), 如果它在凸组合下是个闭集
• $cone(X)$ : $凸锥(convex cone), 如果它在锥组合下是个闭集

仿射子空间可能不是一个向量空间, 因为它有可能不过原点!!!

线性子空间和凸包是已经熟知的概念, 这里提一下对于仿射子空间和凸锥的通俗理解:

仿射子空间

对于一个二维平面, 两个点的仿射子空间就是过这两个点的直线, 此时它是一个一维的概念. 但是如果加入了第三个不共线的点, 此时这三个点的仿射子空间就是整个二维平面了.

由此我推断一个集合的仿射子空间是一个能过所有点的最低维度空间.

凸锥

可以理解成从原点发射的所有能打中凸包的射线组成的集合体, 确实是一个锥的样子, 很形象

Definition 5

函数 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是(向下)凸(convex)的, 如果对于所有的 $x, y \in \mathbb{R}^n$ 和 $\lambda \in[0,1]$ , 满足如下:

$$f(\lambda x+(1-\lambda) y) \leq \lambda f(x)+(1-\lambda) f(y)$$

Lemma 6

如果 $P \subseteq \mathbb{R}^n$ , $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是凸的, 那么 $Q={x \in P \mid f(x) \leq t}$ 也是凸的

?

Definition 7

仿射子空间 $A \subseteq \mathbb{R}^n$ 的维数 $dim(A)$ , 是在 $A$ 中任取一点 $a \in A$ 后, 向量空间 ${x-a \mid x \in A}$ 的维数.

把仿射子空间平移到原点之后的空间的维数.

Definition 8

对于集合 $X \subseteq \mathbb{R}^n$ , $dim(X)$ 的维数和 $aff(X)$ 的维数相同.

Definition 9

集合 $H \subseteq \mathbb{R}^n$ 是一个超平面(hyperplane), 如果存在向量 $a \neq 0$ , $H={x \mid a^T x=b}$.

$a$ 是比当前空间低一维的维度的法向量的方向. 例如: 当前空间是二维平面, 那么 $a$ 就是直线的法向量 ; 当前空间是三维空间, 那么 $a$ 就是平面的法向量. $b$ 是比当前空间低一维的维度的截距, 这是一个有向距离.

Definiation 10

集合 $H^{\prime} \subseteq \mathbb{R}^n$ 是一个(闭)半空间, 如果存在向量 $a \neq 0$ , $H={x \mid a^T x \leq b}$

$a$ 的反方向, 以超平面为界的维度空间

Definition 11

polytop是一个集合 $P \subseteq \mathbb{R}^n$ , 满足 $P=\operatorname{conv}(X)$ , $|X|=c$.

Definition 12

polyhedron是一个集合 $P \subseteq \mathbb{R}^n$ , 这个集合可以被表示成若干个半空间的交集 ${H\left(a_1, b_1\right), \ldots, H\left(a_m, b_m\right)}$, $H\left(a_i, b_i\right)={x \in \mathbb{R}^n \mid a_i x \leq b_i}$

Definition 13

polyhedron $P$ 是有界的(bounded), 如果所有 $x \in P$ , 存在 $B$ , 使得 $|x|_2 \leq B$

Theorem 14

$P$ 是一个有界的polyhedron $\iff$ $P$ 是一个polytop

Definition 15

给定 $P \subseteq \mathbb{R}^n, a \in \mathbb{R}^n$ 和 $b \in \mathbb{R}$. 超平面 $H(a, b)={x \in \mathbb{R}^n \mid a^T x=b}$ 是一个 支撑超平面(supporting hyperplane), 如果 $\max {a^T x \mid x \in P}=b$

那些贴在凸包上的超平面

Definition 16

给定 $P \subseteq \mathbb{R}^n$. $F$ 是一个 $P$ 的face, 如果 $F=P$ 或者对于一些支撑超平面 $H$ , $F=P \cap H$ .

Definition 17

给定 $P$ :

• $v$ 是 $P$ 的一个端点(vertex), 如果 ${ v }$ 是 $P$ 的face
• $e$ 是 $P$ 的一条边(edge), 如果 $e$ 是 $P$ 的face, 并且 $dim(e)=1$
• $F$ 是 $P$ 的一个面(facet), 如果 $F$ 是 $P$ 的face, 并且 $dim(F)=dim(P)-1$

Definition 18

另一种vertex的判断方法:

给定一个polyhedron $P$. 一个点 $x \in P$ 是一个端点(vertex), 如果对于所有的 $y \in P, y \neq x$, $\exists c \in \mathbb{R}^n$ 满足 $c^T y<c^T x$

Definition 19

给定一个polyhedron $P$. 一个点 $x \in P$ 是一个极值点(extreme point), 如果 $\nexists a, b \neq x, a, b \in P$, 满足 $\lambda a+(1-\lambda) b=x$ for $\lambda \in[0,1]$.

不存在与 $x$ 共线并且在 $x$ 两侧的点 $a$ 和 $b$

Definition 20

端点是极值点

Observation

LP的可行域是一个ployhedron

Theorem 21

如果标准形式的LP存在最优解, 那么一定存在一个是极值点的最优解

如果 $x$ 是一个非极值点的最优解

假设有一个向量 $d \neq 0$ , $x \pm d \in P$

$\Rightarrow A \cdot (x \pm d)=b \Rightarrow A \cdot d=0$

在 $d$ 和 $-d$ 中取一个使 $c^T \cdot d’ > 0 \quad (d’ = d \text{ or } -d)$ 的, 作为正方向 $d$. 这是一定可以取到的, 因为 $d \neq 0$ , 若 $c^T \cdot d < 0$, 那么 就一定有 $c^T \cdot d > 0$

现在考虑从 $x$ 出发, 在射线 $x$ 到 $x+d$ 上的点 : $x+\lambda d, \lambda>0$

Case 1: $\exists j$ s.t. $d_j<0$

?

Notation

$B \subseteq{1 \ldots n}$ 是列索引的集合, $A_B$是 $A$ 中索引在 $B$ 里的列的集合

Theorem 22

给定集合 $P={x \mid A x=b, x \geq 0}$. 对于一个 $x \in P$, 定义 $B={j \mid x_j>0}$. 那么 $x$ 是极值点当且仅当 $A_B$ 有线性无关的列.

对于向量 $v1, v_2, … , v_n$ , 若是存在 $a_1, a_2, … , a_n$ , 使得 $\sum{i=1}^n a_i \cdot v_i = 0$ , 则称向量 $v_1, v_2, … , v_n$ 线性相关, 否则向量 $v_1, v_2, … , v_n$ 线性无关

$\Leftarrow$

假设 $x$ 不是极值点

那就存在一个向量 $d \neq 0$ , 使得 $x \pm d \in P$

$\Rightarrow A \cdot (x \pm d)=b \Rightarrow A \cdot d=0 \Rightarrow A\text{ 中的列是线性相关的}$

定义 $B^{\prime}={j \mid d_j \neq 0}$

根据矩阵乘法, $A \cdot d = \sum_i \text{A的第} i \text{列} \cdot d_i$ , 而如果 $d$ 的第 $i$ 个元素是 $0$, 那么他就不会对结果产生贡献.

所以 $A \cdot d$ 的结果其实就是 $A_{B’}$ 中的列依次去乘 $d$ 中的非零元素 (这两者的数量应该是相等的), 乘出来的结果也是 $0$

所以 $A_{B’}$ 的列也是线性相关的

如果对于某个索引 $j$ , $x_j=0 \Rightarrow d_j=0$ , 这是因为有 $x_j \geq 0$ 这个条件.

因此 $B^{\prime} \subseteq B$ , 所以 $A_B$ 的列也必然是线性相关的

$\Rightarrow$

假设 $x$ 是极值点的时候, $A_B$ 是线性相关的

那么就必定存在 $d \neq 0$ , 使得 $A_B \cdot d=0$

将 $d$ 扩展到 $\mathbb{R}^n$ (原本 $d$ 中是只含有 $B$ 中的位置的值的, 现在给其他位置填充 $0$ )

那么 $A \cdot d = 0$

所以对于足够小的 $\lambda$ 有 $x \pm \lambda d \in P$ , 因此 $x$ 不是一个极值点, 与假设矛盾

Theorem 23

给定 $P={x \mid A x=b, x \geq 0}$ , 对任意 $x \in P$ , 我们定义 $B={j \mid x_j>0}$ . 如果 $A_B$ 的列是线性无关的, 则 $x$ 是 $P$ 的一个端点(vertex).

结合Theorem 22, 说明在 $A_B$ 行满秩的前提下, 端点和极值点其实是等价的

定义 $c_j= \begin{cases}0 & j \in B \ -1 & j \notin B\end{cases}$

则 $c^T \cdot x=0$ , 对于其他点 $y \in P$ , $c^T \cdot y \le 0$ (因为 $c$ 是非正的)

根据端点的定义(Definition 18), 如果 $x$ 是端点, 我们必须证明: $\forall y, c^T \cdot y = 0 \Rightarrow x=y$

我们假设 $c^T y=0$ , 则如果 $j \notin B$ , $y_j=0$ 必须满足, 否则结果里面就会出现 $-1$

因为 $y \in P$ , 所以有 $Ay=b$ , 对于 $y$ 中不属于 $B$ 的索引对应的元素, 不会对结果产生贡献, 因为他们是 $0$ , 所以有 $Ay=b=A_B \cdot y_B$ . 对于 $x$ 中不属于 $B$ 的索引对应的元素同理. 所以有 $Ay=b=A_B \cdot y_B = Ax=A_B \cdot x_B$

移项之后能得出: $A_B\left(x_B-y_B\right)=0$

因为 $A$ 的列是线性无关的, 所以 $x_B - y_B$ 一定得是 $0$ (线性无关的定义)

于是就证出了 $\forall y, c^T \cdot y = 0 \Rightarrow x=y$

所以在 $A_B$ 的列是线性无关的条件下, 对于我们构建的 $c$ , $\nexists y \neq x , c^T \cdot y \ge c^T \cdot x$ , 所以 $x$ 必定是端点.

Observation

对于一个LP问题, 我们能够假设矩阵 $A$ 是行满秩的, 即 $\operatorname{rank}(A)=m$

从现在开始, 我们假设标准形式的LP问题的条件矩阵 $A$ 都是行满秩的

假设 $\operatorname{rank}(A)<m$

不失一般性, 我们假设第一行 $A_1$ 能够表示成其他列 $A_2, \ldots, A_m$ 的线性组合:

$$A_1=\sum_{i=2}^m \lambda_i \cdot A_i$$

Case 1

如果 $b1=\sum{i=2}^m \lambda_i \cdot b_i$ , 则第一行就没意义了, 如果除了第一行的其他行能够成立, 那么第一行必定成立

Case 2

如果 $b1 \neq \sum{i=2}^m \lambda_i \cdot b_i$ , 那么LP就是无解的, 因为:

$$A_1 x=\sum_{i=2}^m \lambda_i \cdot A_i x=\sum_{i=2}^m \lambda_i \cdot b_i \neq b_1$$

即如果第一行成立, 则其他行不成立; 如果其他行成立, 则第一行必不成立

Theorem 24

给定 $P={x \mid A x=b, x \geq 0}$ , $x$ 是极值点当且仅当存在 $B \subseteq{1, \ldots, n}$ , 满足 $|B|=m$ 并且:

• $A_B$ 是非奇异的
• $x_B=A_B^{-1} b \geq 0$
• $x_N=0$

定义 $N={1, \ldots, n} \backslash B$

$\Rightarrow$

根据Theorem 22, 如果 $x$ 是极值点, 则存在 $B={j \mid x_j>0}$ , 使得 $A_B$ 的列是线性无关的.

$max\left(|B|\right)=m$ , 因为 $A$ 是行满秩的, 即 $rank(A)=m$ , 并且行秩等于列秩, 所以列秩最大就是 $m$ , 即最多有 $m$ 个线性无关的列.

如果 $|B|<m$ , 我们就往里面加入线性无关的列即可.

易得, 这样构造出的 $B$ 和 $A_B$ 是满足条件的

$\Leftarrow$

上述过程都是充要并且可逆的, 反过来写就好了

Basic Feasible Solutions

如果 $x \in \mathbb{R}^n$ , $A x=b$ 并且定义 $J={j \mid x_j \neq 0}$ , $\operatorname{rank}\left(A_J\right)=|J|$ , 则 $x$ 被称作基本解 (basis solution).

如果 $x$ 是一个基本解, 并且 $x \ge 0$ , 那么 $x$ 被称作基本可行解 (basic feasible solution)

一个底 (basis) 是一个索引集 $B \subseteq{1, \ldots, n}$ , 满足 $\operatorname{rank}\left(A_B\right)=m$ 并且 $|B|=m$

给定底 $B$ , 满足 $A_B x_B=b$ , 并且对于所有 $j \notin B$ , $x_j=0$ 的 $x \in \mathbb{R}^n$ 被称作关联底 $B$ 的基本解

根据Theorem 22, Theorem 23和Theorem 24, 我们知道任何关联底 $B$ 的基本都是一个极值点和端点.

Facts

一个基本可行解满足了约束矩阵 $A$ 中的 $m$ 个等号约束

除此之外, 索引不在底 $B$ 中的 $x$ 的元素 $x_j$ 的值是 $0$ , 因此 $x \ge 0$ 的 $n$ 个非负约束中的 $n-m$ 个被等号满足.

也就是说, 一个基本可行解能等号满足至少 $n$ 个约束

Definition 25

基于上述Facts, 对于一个有 $n$ 个变量的通用LP ($\max {c^T x \mid A x \leq b}$) , $x$ 是一个基本可行解如果 $x$ 是可行的并且存在 $n$ 个 (线性无关的) 约束是被等号满足的 (tight)

Illustration

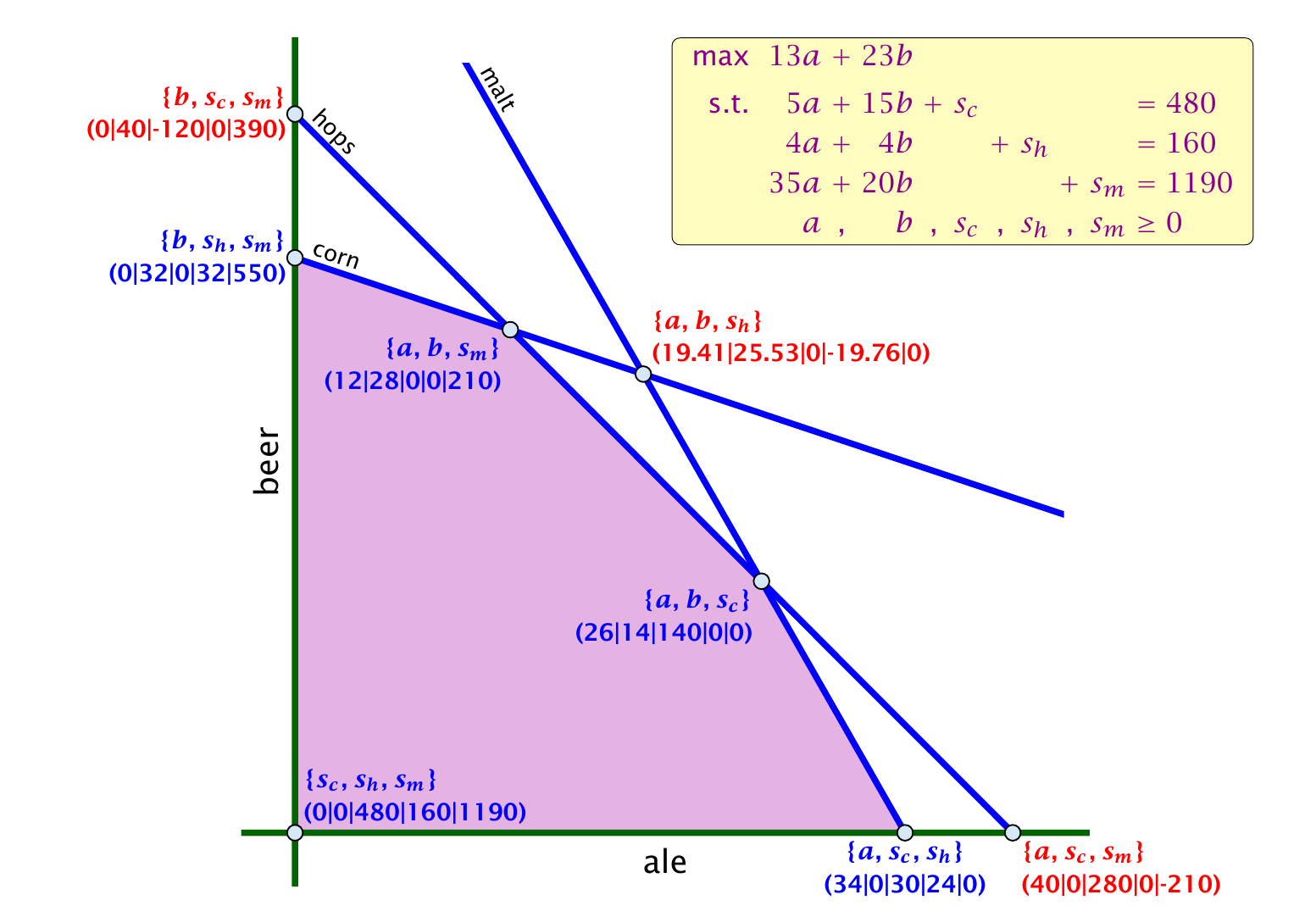
其中蓝色的是基本可行解, 红色的是基本解

Fundamental Questions

Is LP in NP? yes!

因为给定一个底 $B$ , 我们能在多项式时间内计算出他对应的基本解 $A_B^{-1} b$

NP is the set of decision problems for which the problem instances, where the answer is “yes”, have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.

Observation

我们能在 $\mathcal{O}\left(\left(\begin{array}{c}n \ m\end{array}\right) \cdot \operatorname{poly}(n, m)\right)$ 的时间复杂度内计算出最优解

最多只有 $\left(\begin{array}{c}n \ m\end{array}\right)$ 个底, 便利一次计算出最优解即可

如果LP不是有界的, 那么把要求(证)的那个 $c^Tx \leq \alpha$ 也加进去, 就能转换成有界的LP了

Simplex Algorithm

Idea

如果便利所有的基本可行解来求最优解太慢了

我们只需要从一个基本可行解开始, 经过与他相邻 (adjacent) 的基本可行解, 保证目标函数 (objective function) 不减少

两个基本可行解是相邻的, 如果他们对应的底只有一个变量不同

Pivoting Step (Example)

$$\begin{array}{rcrcrcrcrcl} \max \quad 13 a & +&23 b \\ \text { s.t. } \quad 5a & + & 15b & + & s_c & & & & & = & 480 \\ 4a & + & 4b & & & + & s_h & & & = & 160 \\ 35a & + & 20b & & & & & + & s_m & = & 1190 \\ a & , & b & , & s_c & , & s_h &, & s_m & \geq & 0 \end{array}$$

先进行一次小小的变形, 我们要保证在底中的变量 ( ${s_c, s_h, s_m}$ ) 的系数必须是 $1$ , 否则进行一次高斯消元

约束矩阵	状态
$\begin{array}{rcrcrcrcrcrcl} \max \quad Z \\ \text { s.t. } \quad 13 a & + &23 b & & & & & & & - & Z & = & 0 \\ 5a & + & 15b & + & s_c & & & & & & & = & 480 \\ 4a & + & 4b & & & + & s_h & & & & & = & 160 \\ 35a & + & 20b & & & & & + & s_m & & & = & 1190 \\ a & , & b & , & s_c & , & s_h &, & s_m & & & \geq & 0 \end{array} $	$\begin{aligned} & \text {basis}={s_c, s_h, s_m} \\ & a=b=0 \\ & Z=0 \\ & s_c=480 \\ & s_h=160 \\ & s_m=1190\end{aligned}$

这样我们的目标函数就是约束矩阵的第一行了

接下来我们从目标函数中取一个不在底中的并且系数是正的变量(必须是最大的那个, 否则会死循环), 这个例子中可供选择的有 ${a, b}$ , 但是 $b$ 的系数更大, 所以我们选 $b$ , 这变量叫做进入变量 (entering variable)

接下来我们保持 $a=0$ 不变, 增大 $b$ , 因为要维护约束约束矩阵, 所以底中的变量会变小, 我们增大 $b$ 到 $\theta$ 使得有一个底中的变量减小到了 $0$ (不可能有两个, 因为约束矩阵 $A$ 是行满秩的, 如果有两个的话说明 $A$ 的行是线性相关的, 就不是行满秩的了)

这里我们可以很容易的算出 $\theta=\min {480 / 15,160 / 4,1190 / 20}$ , 因为底中的变量的系数都是1

第一个被减到 $0$ 的底中的变量是 $s_c$ , 这个变量叫做离开变量 (leaving variable)

得到了进入变量和离开变量, 我们要对约束矩阵进行变换:

• 在除了第一行 (目标函数) 的行中, 首先将进入变量的系数变为 $1$
• 找到进入变量和离开变量都存在的那行, 消去除了这行的所有行中的进入变量 (这一步的目的是消去其他行不是底中的变量, 让底中的变量只出现一次)
• 更改状态, 将离开变量从底中剔除, 加入进入变量, 根据求得的 $\theta$ 改变变量的值

约束矩阵

状态

$ \begin{array}{rcrcrcrcrcrcl} \max \quad Z \\ \text { s.t. } \quad \frac {16}{3} a & & & - & \frac{23}{15} s_c & & & & & - & Z & = & -736 \\ \frac{1}{3}a & + & b & + & \frac{1}{15}s_c & & & & & & & = & 32 \\ \frac{8}{3} a & & & - & \frac{4}{15}s_c & + & s_h & & & & & = & 32 \\ \frac{85}{3} a & & & - & \frac{4}{3}s_c & & & + & s_m & & & = & 550 \\ a & , & b & , & s_c & , & s_h &, & s_m & & & \geq & 0 \end{array} $

$\begin{aligned} & \text {basis}={b, s_h, s_m} \\ & a=s_c=0 \\ & Z=736 \\ & b=32 \\ & s_h=32 \\ & s_m=550\end{aligned}$

重复以上步骤知道目标函数中的系数都是负的.

这里再走一步:

目标函数中现在只有 $a$ 的系数是负的, 所以我们选择 $a$ 作为进入变量

然后计算 $\theta = \min {3 \cdot 32,3 \cdot 32 / 8,3 \cdot 550 / 85}$ , 这里最小的是第三项, 所以我们选 $s_m$ 作为离开变量

约束矩阵

状态

$ \begin{array}{rcrcrcrcrcrcl} \max \quad Z \\ \text { s.t. } \quad \& & & - & \frac{23}{15} s_c & & - & 2s_h & & & - & Z & = & -800 \\ & + & b & + & \frac{1}{10}s_c & - & \frac{1}{8}s_h & & & & & = & 28 \\ a & & & - & \frac{1}{10}s_c & + & \frac{3}{8}s_h & & & & & = & 12 \\ & & & & \frac{2}{3}s_c & - & \frac{85}{8}s_h & + & s_m & & & = & 210 \\ a & , & b & , & s_c & , & s_h &, & s_m & & & \geq & 0 \end{array} $

$\begin{aligned} & \text {basis}={a, b, s_m} \\ & s_c=s_h=0 \\ & Z=800 \\ & b=28 \\ & a=12 \\ & s_m=210\end{aligned}$

此时目标矩阵中的变量的系数全是负的了, 所以程序结束, 我们找到的最优解是 $800$

Matrix View

$$\begin{array}{rcrcl} c_B^T x_B & + & c_N^T x_N & = & Z \\ A_B x_B & + & A_N x_N & = & b \\ x_B & , & x_N & \geq & 0 \end{array}$$

按照上面说的, 需要把底中的变量的系数变成 $1$ , 并且在约束矩阵中只能出现一次:

$$\begin{array}{rcrcl} & & \left(c_N^T-c_B^T A_B^{-1} A_N\right) x_N & = & Z-c_B^T A_B^{-1} b \\ x_B & + & A_B^{-1} A_N x_N & = & A_B^{-1} b \\ x_B & , & x_N & \geq & 0 \end{array}$$

那么基本可行解就是由 $x_N=0, x_B=A_B^{-1} b$ 组成

如果 $\left(c_N^T-c_B^T A_B^{-1} A_N\right) \leq 0$ , 我们就知道我们已经找到最优解了

Geometric View of Pivoting

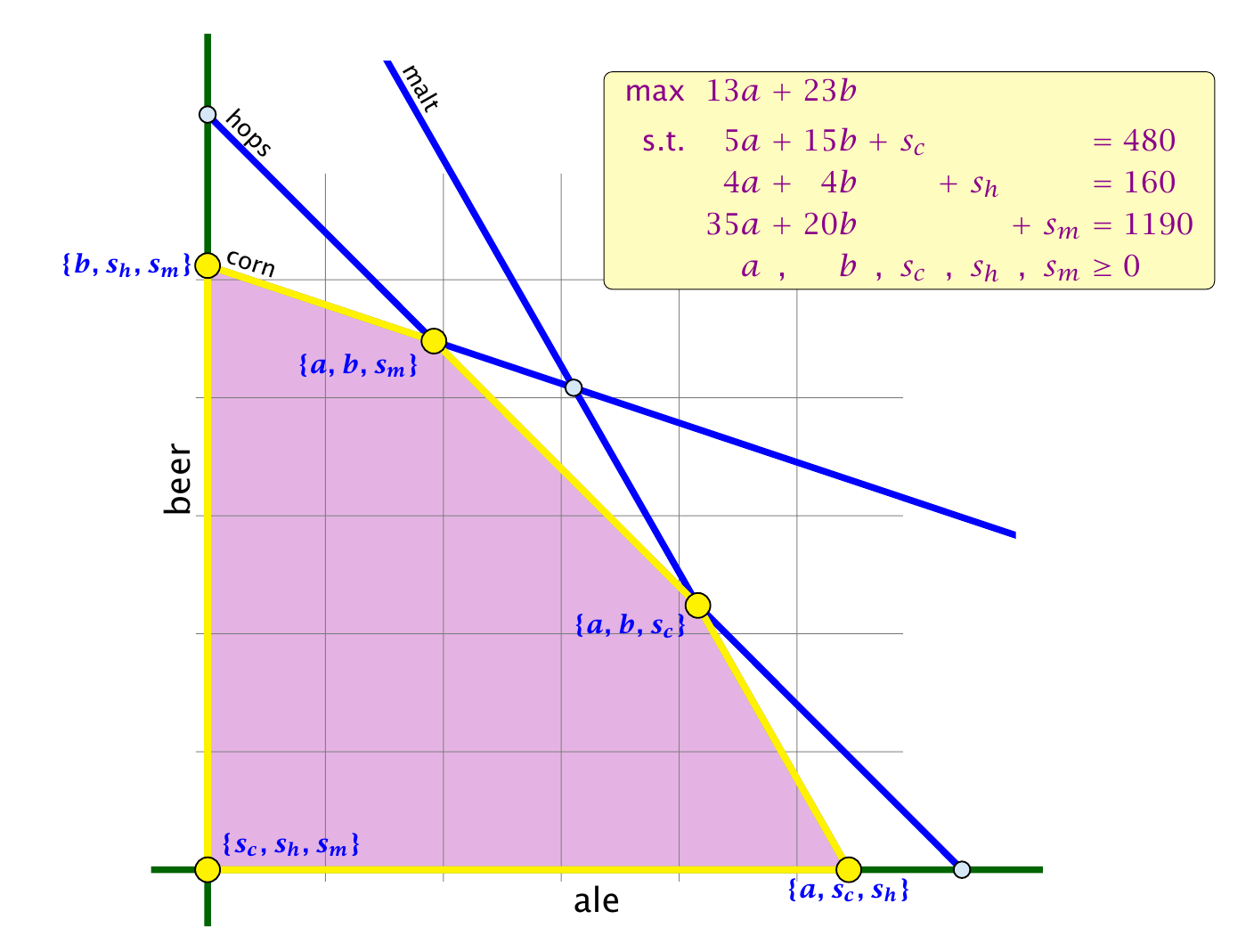
一开始的底在原点, 然后往上走了一步, 再往右走了一步到达最优解

Algebraic Definition of Pivoting

给定底 $B$ 和他关联的基本可行解 $x^*$

选一个索引 $j \notin B$ , 把 $x_j^*$ 从 $0$ 增大到 $\theta \ge 0$

• 其他非底的变量应该不变, 为 $0$
• 底中的变量应该自适应改动以维护约束成立

也就是说从 $x^\ast$ 变成 $x^\ast + \theta \cdot d$

Requirements for $d$

• $d_j = 1$ (归一化)
• $d_{\ell}=0, \ell \notin B, \ell \neq j$
• $A\left(x^*+\theta d\right)=b$ 必须满足, 因为移动后也必须是可行解, 所以我们可以推出 $A d=0$

Definition 26 ( $j$ -th basis direction)

综上, $Ad = AB d_B+A{\ast j}=0$ , $A_{\ast j}$ 是约束矩阵 $A$ 的第 $j$ 列

$AB$ 的列是线性无关的, 所以 $A_B$ 是可逆的, 我们能直接推出 $d_B=-A_B^{-1} A{* j}$

$d_B$ 就是 $j$ -th basis direction

Definition 27 (Reduced Cost)

从 $x^\ast$ 移动到 $x^\ast+\theta \cdot d$ , 目标函数变化了 $\theta \cdot c^T d=\theta\left(cj-c_B^T A_B^{-1} A{\ast j}\right)$

我们定义: $\tilde{c}j=c_j-c_B^T A_B^{-1} A{\ast j}$ 是 $x_j$ 的reduced cost.

reduced cost是对每个 $j$ 都有定义的, 如果 $j \in B$ , 那么 $x_j$ 的reduced cost就是0, 因为我们不能选这个 $j$ 作为进入变量, 所以无法改变目标函数

Matrix View中的 $c_N^T-c_B^T A_B^{-1} A_N$ 就是由 $j \in N$ 的reduced cost构成

Min Ratio Test

Q: What happens if the min ratio test fails to give us a value $θ$
by which we can safely increase the entering variable?

我们知道 $\theta = \min \left( \max \left( bi / A{i e}, 0 \right) \right)$ , 这里的 $A_{i e}$ 是第 $i$ 行中的在底中的变量的值 (具体看上面的步骤)

如果这些值中不是全是负的, 那么这个负值只会增大这个变量, 而不是减小, 所以是没有危险的

如果全是负的, 那么就没有离开变量选择了, LP就不是有界的了

Termination

在Simplex方法的一次迭代中, 目标函数的值是不会下降的, 但是他会保证一直上升吗?

答案是: 并不!

Definition 28 (退化 Degeneracy)

一个基本可行解 $x^\ast$ 是退化的, 如果集合 $J=\left{j \mid x_j^*>0\right}$ 满足 $|J|<m$

若干个基本可行解重合了, 如图右下角有三个点重合了

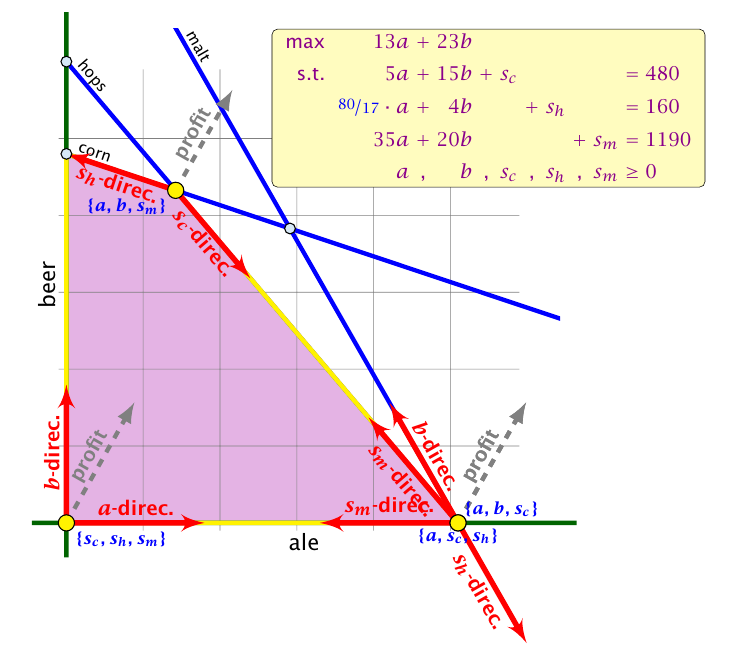
总结: 如何挑选每次迭代中加入到底中的那个下标?

• 我们可以选择一列 $e$ 作为进入变量, 如果 $\tilde{C}_e>0$ ($\tilde{c}_e$ 是 $x_e$ 对应的reduced cost)
• 标准选择是选 $\tilde{c}_e$ 最大的那个列 $e$
• 如果对所有 $i \in{1, \ldots, m}$ 都有 $A_{i e} \leq 0$ , 那说明最大值是无界的
• 否则, 选一个离开变量 $l$ 使得 $b{\ell} / A{\ell e}$ 在所有的 $A_{i e}>0$ 是最小的
• 如果有数个变量都同时是最小值, 那就到了一个退化的基本可行解
• 取决于 $l$ 的选取, Simplex方法可能会陷入死循环

一些感悟: 约束矩阵 $A$ 中的每一行都能代表一个在底中的变量, 而 $A$ 中的每一列代表一个变量, 因为 $A$ 是行满秩的

What do we have so far?

Suppose we are given an initial feasible solution to an LP. If the LP
is non-degenerate then Simplex will terminate.
Note that we either terminate because the min-ratio test fails and
we can conclude that the LP is unbounded, or we terminate
because the vector of reduced cost is non-positive. In the latter
case we have an optimum solution.

Initial Solution

TODO

Lemma 29 (Optimality)

有一个底 $B$ 和一个基于 $B$ 的基本可行解 $x^\ast$ , $\tilde{c} \leq 0$ 能够得出 $x^\ast$ 是LP的最优解

Definition 30 (Duality)

主要线性规划(primal LP) $z=\max \left{c^T x \mid A x \leq b, x \geq 0\right}$ 的对偶问题(dual problem) 是 $w=\min \left{b^T y \mid A^T y \geq c, y \geq 0\right}$

Lemma 31

一个主要线性规划问题的对偶问题的对偶问题是他自己

$\begin{aligned} & w=\min \left{b^T y \mid A^T y \geq c, y \geq 0\right} \ & w=-\max \left{-b^T y \mid-A^T y \leq-c, y \geq 0\right}\end{aligned}$

$w$ 的对偶问题是:

$\begin{aligned} & z=-\min \left{-c^T x \mid-A x \geq-b, x \geq 0\right} \ & z=\max \left{c^T x \mid A x \leq b, x \geq 0\right}\end{aligned}$

Theorem 32 (Weak Duality)

$z=\max \left{c^T x \mid A x \leq b, x \geq 0\right}$ 和 $w=\min \left{b^T y \mid A^T y \geq c, y \geq 0\right}$ 是一对对偶问题, $x$ 是主要可行(primal feasible), 当且仅当 $x \in{x \mid A x \leq b, x \geq 0}$ ,
$y$ 是对偶可行(dual feasible), 当且仅当 $y \in\left{y \mid A^T y \geq c, y \geq 0\right}$

给定 $\hat{x}$ 是主要可行的, $\hat{y}$ 是对偶可行的:

$$c^T \hat{x} \leq z \leq w \leq b^T \hat{y}$$

$$A^T \hat{y} \geq c \Rightarrow \hat{x}^T A^T \hat{y} \geq \hat{x}^T c\quad (\hat{x} \geq 0)$$ $$A \hat{x} \leq b \Rightarrow y^T A \hat{x} \leq \hat{y}^T b \quad (\hat{y} \geq 0)$$

通过这两个能推出:

$$c^T \hat{x} \leq \hat{y}^T A \hat{x} \leq b^T \hat{y}$$

又因为 $z$ 是主要可行的最大解, $w$ 是对偶可行的最小解, 就有: $z \leq w$

另外: 如果主要线性规划问题 $P$ 是无界的, 那么其对偶问题 $D$ 就是不可行的

Simplex and Duality

$z =\max \left{c^T x \mid A x=b, x \geq 0\right} $

$w =\min \left{b^T y \mid A^T y \geq c\right}$

是一组对偶问题, 这也代表: 在解一个主要线性规划问题的对偶问题的时候, 我们没有变量非负的限制

对主要线性规划问题进行改写:

$\begin{aligned} \max & \left{c^T x \mid A x=b, x \geq 0\right} \\ & =\max \left{c^T x \mid A x \leq b,-A x \leq-b, x \geq 0\right} \\ & =\max \left{c^T x \mid\left[\begin{array}{c}A \\ -A\end{array}\right] x \leq\left[\begin{array}{c}b \\ -b\end{array}\right], x \geq 0\right}\end{aligned}$

这里的最后一步就是把两个不等式写成矩阵形式

改写后的对偶问题为:

$\begin{aligned} \min & \left{\left[b^T-b^T\right] y \mid\left[A^T-A^T\right] y \geq c, y \geq 0\right} \\ & =\min \left{\left[b^T-b^T\right] \cdot\left[\begin{array}{c}y^{+} \\ y^{-}\end{array}\right] \mid\left[A^T-A^T\right] \cdot\left[\begin{array}{l}y^{+} \\ y^{-}\end{array}\right] \geq c, y^{-} \geq 0, y^{+} \geq 0\right} \\ & =\min \left{b^T \cdot\left(y^{+}-y^{-}\right) \mid A^T \cdot\left(y^{+}-y^{-}\right) \geq c, y^{-} \geq 0, y^{+} \geq 0\right} \\ & =\min \left{b^T y^{\prime} \mid A^T y^{\prime} \geq c\right}\end{aligned}$

Proof of Optimality Criterion for Simplex

假设我们有一个基本可行解 $x^\ast$, 其reduced cost为:

$\tilde{c}=c^T-c_B^T A_B^{-1} A \leq 0$

这也代表 $x^ast$ 是最优解 (Lemma 29)

我们对这个式子进行改写: $A^T\left(A_B^{-1}\right)^T c_B \geq c$

令 $y^\ast=\left(A_B^{-1}\right)^T c_B$

$\begin{aligned} b^T y^\ast & =\left(A x^\ast\right)^T y^\ast=\left(A_B x_B^\ast\right)^T y^\ast \\ & =\left(A_B x_B^\ast\right)^T\left(A_B^{-1}\right)^T c_B=\left(x_B^\ast\right)^T A_B^T\left(A_B^{-1}\right)^T c_B \\ & =c^T x^\ast\end{aligned}$

因为 $c^T \hat{x} \leq z \leq w \leq b^T \hat{y}$ 所以 $y^\ast$ 其实也是最优解

所以在 $x^\ast$ 和 $y^\ast$ 都是最优解的情况下, 对偶差距(Duality Gap)为 $0$

Strong Duality

$P=\max \left{c^T x \mid A x \leq b, x \geq 0\right}$

$n_A$ : 变量的个数( $A$ 的列数), $m_A$ : 约束的个数 ( $A$ 的行数)

我们也可以把变量非负这个约束加入约束矩阵 $A$ ( $ x \geq 0 \Rightarrow -x \leq 0$ )

然后新的LP: $\bar{P}=\max \left{c^T x \mid \bar{A} x \leq \bar{b}\right}$

$n{\bar{A}}=n_A, m{\bar{A}}=m_A+n_A$

新LP的对偶问题: $D=\min \left{\bar{b}^T y \mid \bar{A}^T y=c, y \geq 0\right}$

Theorem 33 (Strong Duality)

给定 $P$ 和 $D$ 互为对偶问题对, $z^\ast$ 和 $w^\ast$ 是这对问题的最优解, 那么:

$$z^\ast = w^\ast$$

Lemma 34 (Weierstrass)

给定 $X$ 是一个凸集, $f(x)$ 是在凸集 $X$ 上的一个连续的函数, 那么 $\min {f(x): x \in X}$ 存在

Lemma 35 (Projection Lemma)

给定 $X \subseteq \mathbb{R}^m$ 是一个非空的凸集, 并且 $y \notin X$. 那就存在一个凸集上到 $y$ 的距离最近的点 $x^\ast$ . 并且, 对所有 $x \in X$ , 都有 $\left(y-x^\ast\right)^T\left(x-x^\ast\right) \leq 0$

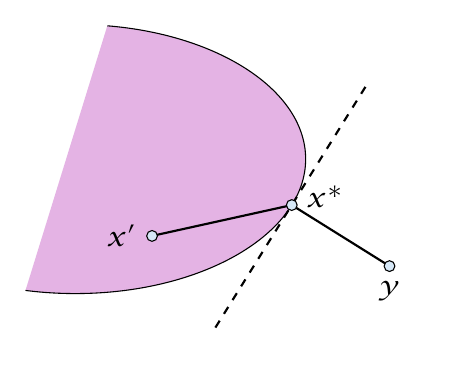
$f(x)=|y-x|$

但是此时还不能用Lemma 34, 因为 $X$ 可能不是有界的

解决方法: 因为 $X \neq \varnothing$ , 所以存在一个点 $x’ \in X$ , 定义 $X^{\prime}=\left{x \in X \mid|y-x| \leq\left|y-x^{\prime}\right|\right}$ , 此时这个 $X’$ 就是闭合的(closed)并且有界的(bounded)

这样我们就可以通过Lemma 34证明: 最近点必定存在.

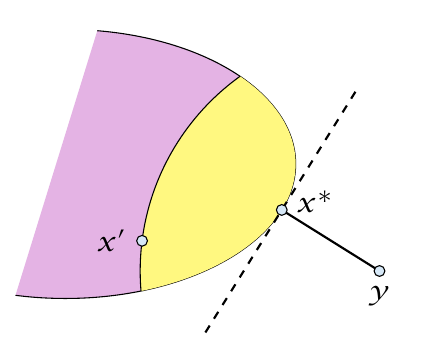
接下来证明 $\left(y-x^\ast\right)^T\left(x-x^\ast\right) \leq 0$

假设 $x^\ast$ 是最近点. 所以 对所有的 $x \in X$ , $\left|y-x^\ast\right|^2 \leq|y-x|^2$

根据凸集的性质: $x \in X$ 那么 对于所有的 $0 \leq \epsilon \leq 1$ , $x^\ast+\epsilon\left(x-x^\ast\right) \in X$ ( $x$ 和 $x’$ 的连线上的点)

$$\begin{aligned} \left\|y-x^\ast\right\|^2 & \leq\left\|y-x^\ast-\epsilon\left(x-x^\ast\right)\right\|^2 \\\\ & =\left\|y-x^\ast\right\|^2+\epsilon^2\left\|x-x^\ast\right\|^2-2 \epsilon\left(y-x^\ast\right)^T\left(x-x^\ast\right) \end{aligned}$$

改写一下上面的式子: $\left(y-x^\ast\right)^T\left(x-x^\ast\right) \leq \frac{1}{2} \epsilon\left|x-x^\ast\right|^2$

如果 $\epsilon \rightarrow 0$ 就得到了我们要证明的结论

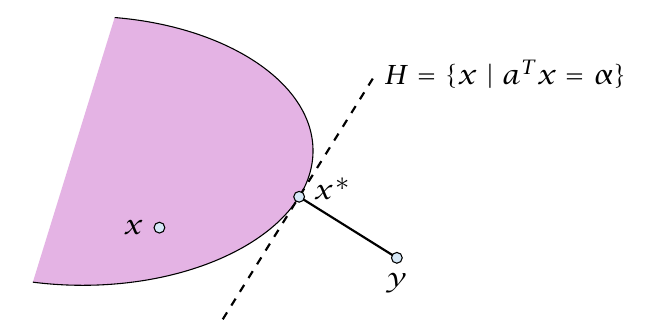
Theorem 36 (Separating Hyperplane)

给定 $X \subseteq \mathbb{R}^m$ 是一个非空的凸集, 并且 $y \notin X$. 那么一定存在一个分割超平面 $\left{x \in \mathbb{R}: a^T x=\alpha, a \in \mathbb{R}^m, \alpha \in \mathbb{R} \right}$ 将 $X$ 和 $y$ 分割开 (对于所有的 $x \in X$, $a^T y<\alpha ; a^T x \geq \alpha$)

$x^\ast \in X$ 是 $X$ 中距离 $y$ 的最近点

根据上面的定理, 对于所有的 $x \in X$, $\left(y-x^\ast\right)^T\left(x-x^\ast\right) \leq 0$

令: $a=\left(x^\ast-y\right)$ , $\alpha=a^T x^\ast$

对于所有的 $x \in X: a^T\left(x-x^\ast\right) \geq 0$ , 所以有 $a^T x \geq \alpha$

同时 $a^T y=a^T\left(x^\ast-a\right)=\alpha-|a|^2<\alpha$

Lemma 37 (Farkas Lemma)

给定 $A$ 是一个 $m \times n$ 的矩阵, 那么下面两个陈述仅有一个是真的:

• $\exists x \in \mathbb{R}^n$ , $A x=b, x \geq 0$
• $\exists y \in \mathbb{R}^m$ , $A^T y \geq 0, b^T y<0$

首先我们先证明上述两个陈述最多有一个是正确的

假设 $\hat{x}$ 满足第一天陈述, $\hat{y}$ 满足第二条, 那么有

$$0>y^T b=y^T A x \geq 0$$

所以不能两条都同时满足

现在假设第一条不满足

$S={A x: x \geq 0}$ 是矩阵 $A$ 的列的锥组合, 所以 $S$ 是闭合的, 凸的. 因为第一条不满足, 所以 $Ax \neq b$ , 所以 $b \notin S$

我们想要证明存在一个 $y$ , 满足 $A^T y \geq 0, b^T y<0$

让 $y$ 是分割 $b$ 和 $S$ 的半平面, 因此: $y^T b<\alpha$ 并且对于所有的 $s \in S$ , $y^T s \geq \alpha$

$0 \in S \Rightarrow y^T \cdot 0 \geq \alpha \Rightarrow \alpha \leq 0 \Rightarrow y^T b<0$

对于 $x \geq 0$ , $y^T A x \geq \alpha$ , 因此 $y^T A \geq 0$ (我们能随意指定 $x \geq 0$ )

Lemma 38 (Farkas Lemma; different version)

将两个陈述重写一下:

• $\exists x \in \mathbb{R}^n$ , $[A \quad I] \cdot\left[\begin{array}{c}x \\ s\end{array}\right]=b, x \geq 0, s \geq 0$
• $\exists y \in \mathbb{R}^m$ , $\left[\begin{array}{c}A^T \ I\end{array}\right] y \geq 0, b^T y<0$

Proof of Strong Duality

讲了这么就的辅助定理, 正菜终于端上来了

$P: z=\max \left{c^T x \mid A x \leq b, x \geq 0\right} $

$D: w=\min \left{b^T y \mid A^T y \geq c, y \geq 0\right}$

Theorem 39 (Strong Duality) 同Theorem 33

$\boldsymbol{z} \leq \boldsymbol{w}$ :

weak duality已经证明了

$z \geq w$ :

我们证明 $z<\alpha$ 能够推出 $w<\alpha$

$\begin{array}{rrcr} \exists x \in \mathbb{R}^n & \\ \text { s.t. } & A x & \leq & b \\ & -c^T x & \leq & -\alpha \\ & x & \geq & 0 \end{array}$	$\begin{array}{rrcr} \exists y \in \mathbb{R}^m ; v \in \mathbb{R} & \\ \text { s.t. } & A^T y-c v & \geq & 0 \\ & b^T y-\alpha v & < & 0 \\ & y, v & \geq & 0\end{array}$

因为我们这里假设的 $z<\alpha$ , 又因为 $z$ 是 $c^T x$ 的最大值, 所以 $c^T x$ 是不可能大于等于 $\alpha$ 的, 所以左边的不等式组是不可能被满足的, 根据Farkas Lemma, 那么右边的一定是可满足的

如果解 $y, v$ 满足 $v=0$ , 那么我们就可以推出

$$\begin{array}{rrcr}\exists y \in \mathbb{R}^m & \\\\ \text { s.t. } & A^T y & \geq & 0 \\\\ & b^T y & < & 0 \\\\ & y & \geq & 0\end{array}$$

是可满足的

这玩意儿的根据Farkars Lemma对应的那个不等式组其实就是原来的LP, 因此我们就推出原来的LP是不可能被满足的, 而我们假设LP应该是有解的, 所以 $v \neq 0$ 必须满足

因此存在一个解 $y, v$ 满足 $v>0$

那么我们缩放整个不等式组 (同时缩放 $y$ 和 $v$), 让 $v=1$

$$\begin{array}{rrcr} \exists y \in \mathbb{R}^m ; v \in \mathbb{R} & \\\\ \text { s.t. } & A^T y & \geq & c \\\\ & b^T y & < & \alpha \\\\ & y & \geq & 0 \\\\ & v & = & 1\end{array}$$

因为这个不等式组是有解的, 因此存在 $y$ , $b^T y<\alpha$ , 因为 $w$ 是 $b^T y$ 的最小值, 所以有 $w<\alpha$ , 得证

所以怎么推出 $z \geq w$ 来的 ?

Lemma 41 (Complementary Slackness)

假设LP $P=\max \left{c^T x \mid A x \leq b ; x \geq 0\right}$ 有解 $x^$ , 他的对偶问题 $D=\min \left{b^T y \mid A^T y \geq c ; y \geq 0\right}$ 有解 $y^$ , 那么:

1. 如果 $x_j^*>0$ 那么 $D$ 中第 $j$ 个约束是等号满足的
2. 如果 $D$ 中第 $j$ 个约束不是等号满足的, 那么$x_j^*=0$
3. 如果 $y_i^*>0$ 那么 $P$ 中第 $i$ 个约束是等号满足的
4. 如果 $P$ 中第 $i$ 个约束不是等号满足的, 那么$x_i^*=0$

TODO: 写完这个

TODO: Interpretation of Dual Variables