传送门：Guess the Cycle Size

给你一个无向环形图，图上有$n(3 \leq n \leq 10^{18})$个节点，一次能询问两个点之间的距离，但是返回的是两个距离中的任意一个，在只有$50$次的询问下，问环的长度是多少。

传送门：Sheikh

给定一串长度为$n(1 \leq n \leq 10^5)$的数列$a1, a_2, \ldots, a_n\left(0 \leq a_i \leq 10^9\right)$，定义$f(l, r)=\operatorname{sum}(l, r)-\operatorname{xor}(l, r)$，其中$\operatorname{sum}(l, r)=a_l+a{l+1}+\ldots+ar$，$\operatorname{xor}(l, r)=a_l \oplus a{l+1} \oplus \ldots \oplus a_r$，一共有$q$次询问，每次询问会给定一个区间，询问这个区间内满足$f$最大的最短的子段。

传送门：Slime Escape

一条直线上有$n(3 \leq n \leq 200000)$个史莱姆，你能控制第$k(1 \leq k \leq n)$个，第$i$个史莱姆的生命值是$a_i$。

现在你可以控制这个史莱姆向左或者向右“吞噬”别的史莱姆，你每“吞噬”一个史莱姆$i$，你控制的史莱姆的生命值会增加$a_i$，但是有的史莱姆的生命值是负的，一旦你控制的史莱姆的生命值也变成负的话，你就输掉了游戏。

通关的目标是走到最左边或者走到最右边，问你有没有可行的解。

传送门：Range = √Sum

给定一个正整数$n(1 \leq n \leq 3 \cdot 10^5)$，找出一串$n$个不同的数的数列$a_1, a_2, … , a_n(1 \leq a_i \leq 10^9)$，满足以下式子：

$$\max \left(a_1, a_2, \ldots, a_n\right)-\min \left(a_1, a_2, \ldots, a_n\right)=\sqrt{a_1+a_2+\cdots+a_n}$$

传送门：All Possible Digits

给定一个数字$n(1 \leq n \leq 100)$，进制$p(2 \leq p \leq 10^9)$，并且给出这个数在$p$进制下的表示。现在有一个操作，即给这个数加上1，问要操作几次才能让$p$进制下的所有数位都出现一次？

传送门：Shuffle

给定一个二进制字符串，你可以对这个字符串进行最多一次如下的操作：

从$s$中选择一个正好有$k$个1字符的子串，然后你可以随意的打乱它。

计算可以从$s$经过这样一次操作之后能得到的不同的字符串的数量之和

传送门：The Strongest Build

你有$n$个物品槽，每个物品槽可以存放一个物品。现在对于每个物品槽，有若干个物品可以选择，但是有$m$个物品组合是被禁用的。每个物品有一个价值，求没被禁用的物品组合的最大价值之和是哪个物品组合。

物品组合：当这$n$个物品槽都选定一个物品后，这$n$个物品构成一个物品组合。

传送门: F. Maximum White Subtree

给予你一颗无根树，树上的节点被染成黑色或者白色，求对于某一个节点，在任意包含这个节点的子树中，问白色的节点数量最多能比黑色节点多多少个？

例：

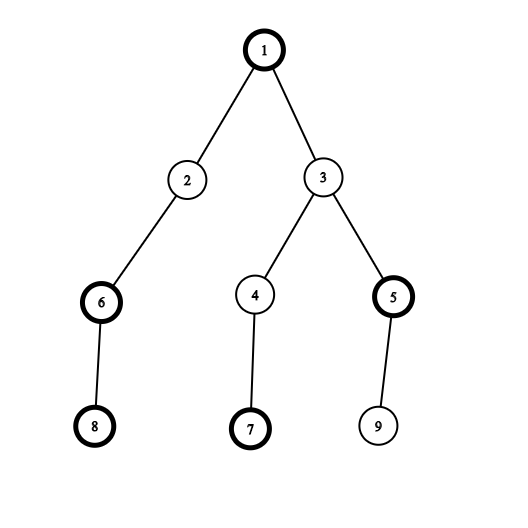
黑色节点为加粗边框的节点

对于节点4，答案为2，选的子树为$(3,4)$

代数结构(algebraische Strukturen)

半群(Halbgruppe)

一个半群是一种代数结构$\left\langle A, \bullet^{2}\right\rangle$, 其具有如下的性质:

• 满足结合律, 也就是说$\forall a, b, c:(a \cdot(b \bullet c))=((a \cdot b) \cdot c)$

 

一个可换的的半群还需满足如下性质:

• 满足交换律, 也就是说$\forall a, b:(a \cdot b)=(b \bullet a)$

 

幺半群(Monoid)

一个(可换的)幺半群是一种代数结构$\left\langle A, \bullet^{2}, 1^{0}\right\rangle$, 其具有如下性质:

• $\left\langle A, \bullet^{2}\right\rangle$是一个(可换的)半群
• 存在单位元(neutrales Element): $1^{0} ($关于$\bullet)$

在半群的基础上新加了**单位元$1^{0}$的需求**

 

群(Gruppe)

一个(可换的)群是一种代数结构$\left\langle A, \bullet^{2}, 1^{0}\right\rangle$, 其具有以下性质:

• $\left\langle A, \bullet^{2}, 1^{0}\right\rangle$是一个(可换的)幺半群
• 存在逆元(关于$\bullet$), 也就是说$\forall a \exists b:(a \cdot b)=1=(b \cdot a)$

在幺半群的基础上新加了**元素的逆元存在需求**

 

一个可换的群也被称作阿贝尔群(abelsche Gruppe)

 

环(Ring)

一个(伪)环是一个代数结构$\left\langle A,+^{2}, \bullet^{2}, 0^{0}\right\rangle$ (或者$\left\langle A,+^{2}, \bullet^{2}, 0^{0}, 1^{0}\right\rangle$), 其具有以下性质:

• $\left\langle A, \bullet^{2}\right\rangle$是一个半群(或者$\left\langle A, \bullet^{2}, 1^{0}\right\rangle$是一个幺半群)
• $\left\langle A,+^{2}, 0^{0}\right\rangle$是一个可换的群
• 从两个方向满足交换律, 也就是说$\forall a, b, c:(a \cdot(b+c))=(a \bullet b+a \cdot c)$并且$((a+b) \cdot c)=((a \cdot c)+(b \cdot c))$

在群的基础上新增了对于**交换律的需求**

 

域(Körper)

一个域是一个代数结构$\left\langle A,+^{2}, \bullet^{2}, 0^{0}, 1^{0}\right\rangle$, 其具有以下性质:

• $\left\langle A,+^{2}, \bullet^{2}, 0^{0}, 1^{0}\right\rangle$是一个伪环
• $\left\langle A \backslash{0}, \bullet^{2}, 1^{0}\right\rangle$是一个可换的群

以上所有性质都有, 并且新增了对于**非0单位有逆元的需求**